Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. lấy điểm B bất kì thuộc đường thằng d. Bài 68 trang 102 sgk toán 8 tập 1 - Đường thẳng song song với một đường thẳng cho trước
Bài 68. Cho điểm \(A\) nằm ngoài đường thẳng \(d\) và có khoảng cách đến \(d\) bằng \(2cm\). lấy điểm \(B\) bất kì thuộc đường thẳng \(d\). Gọi \(C\) là điểm đối xứng với điểm \(A\) qua điểm \(B\). Khi điểm \(B\) di chuyển trên đường thẳng \(d\) thì điểm \(C\) di chuyển trên đường nào ?
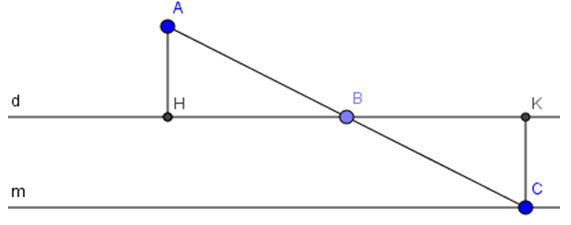
Kẻ \(AH\) và \(CK\) vuông góc với \(d\).
Ta có \(AB = CB\) (vì \(C\) là điểm đối xứng với \(A\) qua \(B\))
Advertisements (Quảng cáo)
\(\widehat{ABH}\) = \(\widehat{CBK}\) ( đối đỉnh)
nên \(∆AHB = ∆CKB\) (cạnh huyền - góc nhọn)
Suy ra \(CK = AH = 2cm\)
Điểm \(C\) cách đường thẳng \(d\) cố định một khoảng cách không đổi \(2cm\) nên \(C\) di chuyển trên đường thẳng \(m\) song song với \(d\) và cách \(d\) một khoảng bằng \(2cm\).