Cho góc vuông xOy, điểm A thuộc tia Oy sao cho OA = 2cm. Lấy B là một điểm bất kì thuộc tia. Bài 70 trang 103 sgk toán 8 tập 1 - Đường thẳng song song với một đường thẳng cho trước
Bài 70. Cho góc vuông \(xOy\), điểm \(A\) thuộc tia \(Oy\) sao cho \(OA = 2cm\). Lấy \(B\) là một điểm bất kì thuộc tia \(Ox\). Gọi \(C\) là trung điểm của \(AB\). Khi điểm \(B\) di chuyển trên tia \(Ox\) thì điểm \(C\) di chuyển trên đường nào ?
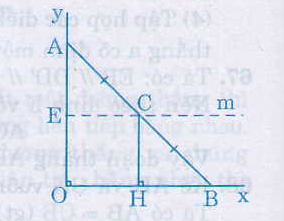
Kẻ \(CH ⊥ Ox\)
Ta có \(CB = CA\) (vì \(C\) là trung điểm của \(AB\))
Advertisements (Quảng cáo)
\(CH // AO\) (cùng vuông góc \(Ox\))
Mặt khác \(C\) là trung điểm của \(AB\) nên \(CH\) là đường trung bình của tam giác \(ABO\)
Suy ra \(CH = \frac{1}{2}AO = \frac{1}{2}.2 = 1 (cm)\)
Điểm \(C\) cách tia \(Ox\) cố định một khoảng không đổi \(1cm\) nên \(C\) di chuyển trên tia \(Em\) song song với \(Ox\) và cách \(Ox\) một khoảng bằng \(1cm\).