Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.. Bài 75 trang 106 sgk toán 8 tập 1 - Hình thoi
Bài 75. Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.

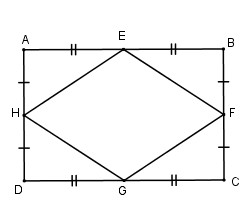
Giả sử hình chữ nhật \(ABCD\) có \(E,F,G,H\) lần lượt là trung điểm của \(AB,BC,CD,DA\)
Bốn tam giác vuông \(EAH, EBF, GDH, GCF\) có:
Advertisements (Quảng cáo)
\(AE = BE = DG = CG\) ( = \(\frac{1}{2}AB\) = \(\frac{1}{2}CD\) )
\(HA = FB = DH = CF\) ( = \(\frac{1}{2}AD = \frac{1}{2}BC\) )
Suy ra \(∆EAH = ∆EBF = ∆GDH = ∆GCF (c.g.c)\)
Suy ra \(EH = EF = GH = GF\)
Vậy \(EFGH\) là hình thoi (theo định nghĩa)
