Bài 76 trang 106 Toán 8 tập 1, Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật...

76. Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.

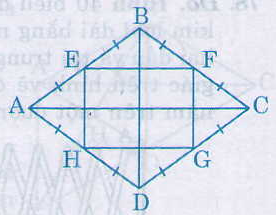
Ta có: EB = EA, FB = FA (gt)

nên EF là đường trung bình của ∆ABC.

Do đó EF // AC

HD = HA, GD = GC (gt)

nên HG là đường trung bình của ∆ADC.

Do đó HG // AC

Suy ra EF // HG       (1)

Chứng minh tương tự EH // FC    (2)

Từ (1) (2) ta được EFGH là hình bình hành.

Lại có EF // AC và BD ⊥ AC nên BD ⊥ EF

EH // BD và EF ⊥ BD nên EF ⊥ EH

nên \(\widehat{FEH}\) = 90⁰

Hình bình hành EFGH có \(\widehat{E}\) = 90⁰ nên là hình chữ nhật.