Bài 82. Cho hình 107, trong đó \(ABCD\) là hình vuông. Chứng minh rằng tứ giác \(EFGH\) là hình vuông.
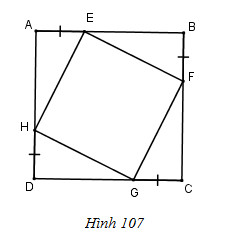

Các tam giác vuông \(AEH, BFE, CGF, DHG\) có:
\(AE = BF = CG = DH\) (1) (gt)
Theo giả thiết \(ABCD\) là hình vuông nên \(AB=BC=CD=DA\) (2)
Từ (1) và (2) suy ra \(AH = BE = CF = DG\)
Nên \(∆AEH = ∆BFE = ∆CGF = ∆DHG\) (c.g.c)
Advertisements (Quảng cáo)
Do đó
\(HE = EF = FG = GH\) ( các cạnh tương ứng)
và \(\widehat{EHA}\) = \(\widehat{FEB}\) (hai góc tương ứng bằng nhau)
Ta có \(\widehat{HEF} = 180^0- (\widehat{HEA}\) + \(\widehat{FEB}) \)
\(= 180^0- (\widehat{HEA}\) + \(\widehat{EHA})\)
\(= 180^0- 90^0= 90^0\) (Vì tam giác \(AHE\) vuông nên \((\widehat{HEA}\) + \(\widehat{EHA})=90^0\))
Tứ giác \(EFGH\) có bốn cạnh bằng nhau và một góc vuông nên là hình vuông.
