
Quan sát hình 9.
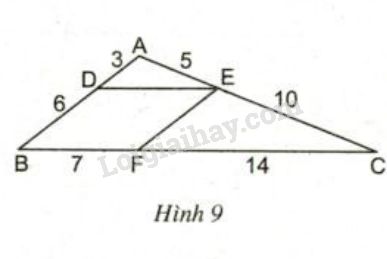
a) Trong hình đã cho có bao nhiêu cặp đường thẳng song song với nhau?
b) Tứ giác \(BDEF\) là hình gì?
c) So sánh các tỉ số \(\dfrac{{AD}}{{AB}};\dfrac{{AE}}{{AC}};\dfrac{{DE}}{{BC}}\) và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác \(ADE\) và \(ABC\).
Sử dụng định lí Ta-lét đảo; dấu hiệu nhận biết, tính chất hình bình hành

a) Ta có:
\(\begin{array}{l}\dfrac{{AD}}{{AB}} = \dfrac{3}{{3 + 6}} = \dfrac{3}{9} = \dfrac{1}{3}\\\dfrac{{AE}}{{AC}} = \dfrac{5}{{5 + 10}} = \dfrac{5}{{15}} = \dfrac{1}{3}\\ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\end{array}\)
Advertisements (Quảng cáo)
Theo định lí Ta- lét đảo thì \(DE//BC\)
\(\begin{array}{l}\dfrac{{CE}}{{CA}} = \dfrac{{10}}{{10 + 5}} = \dfrac{{10}}{{15}} = \dfrac{2}{3}\\\dfrac{{CF}}{{CB}} = \dfrac{{14}}{{14 + 7}} = \dfrac{{14}}{{21}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{CE}}{{CA}} = \dfrac{{CF}}{{CB}}\end{array}\)
Theo định lí Ta-lét đảo thì \(EF//AB\)
Trong hình vẽ đã cho có 2 cặp đường thẳng song song với nhau.
b) Tứ giác \(BDEF\) có \(BD//EF;DE//BF\) nên \(BDEF\) là hình bình hành.
c) Vì \(BDEF\) là hình bình hành nên \(DE = BF = 7\) (Tính chất hình bình hành).
Ta có: \(\dfrac{{DE}}{{BC}} = \dfrac{7}{{7 + 14}} = \dfrac{1}{3}\)
Do đó: \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}} = \dfrac{1}{3}\)
Nhận xét: Hai tam giác \(ADE\) và \(ABC\) có các cặp cạnh tương ứng tỉ lệ.
