
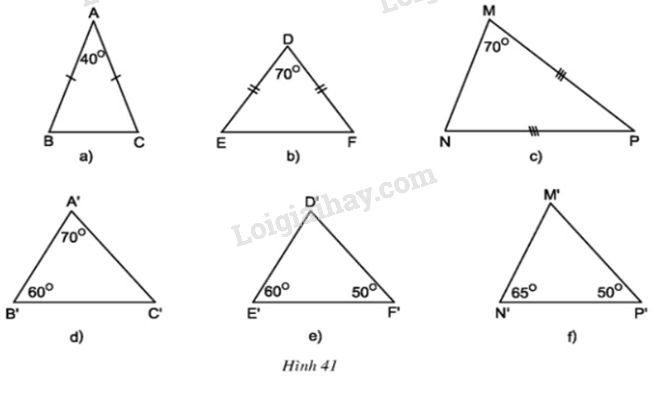
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
Áp dụng định lí
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng

\(ΔABC\) có \(\widehat A + \widehat B + \widehat C = {180^o}\)
Mà \(ΔABC\) cân tại \(A \Rightarrow \widehat B = \widehat C\)
\( \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\)
Advertisements (Quảng cáo)
\(\Rightarrow \widehat B = \widehat C = \dfrac{{\left( {{{180}^o} - {{40}^o}} \right)}}{2} = {70^o}\)
\(ΔMNP\) cân tại \(P \Rightarrow \widehat M = \widehat N = {70^o}\)
\(ΔABC\) và \(ΔPMN\) có
\(\eqalign{& \widehat B = \widehat M = {70^o} \cr & \widehat C = \widehat N = {70^o} \cr & \Rightarrow \Delta ABC \text{ đồng dạng } \Delta PMN\,\,\left( {g.g} \right) \cr} \)
\(\Delta A’B’C’\) có \(\widehat {A’} + \widehat {B’} + \widehat {C’} = {180^o}\)
\( \Rightarrow \widehat {C’} = {180^o} - \left( {\widehat {A’} + \widehat {B’}} \right) \)\(\,= {180^o} - \left( {{{70}^o} + {{60}^o}} \right) = {50^o}\)
\(ΔA’B’C’\) và \(ΔD’E’F’\) có
\(\eqalign{& \widehat {B’} = \widehat {E’} = {60^o} \cr & \widehat {C’} = \widehat {F’} = {50^o} \cr & \Rightarrow \Delta A’B’C’ \text{ đồng dạng } \Delta D’E’F’\,\,\left( {g.g} \right) \cr} \)
