Câu hỏi/bài tập:

Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.
a) Tính độ dài các đoạn thẳng DB và DC.
b) Tính tỉ số diện tích của hai tam giác ABD và ACD.

- Sử dụng tính chất đường phân giác của tam giác.
- Sử dụng công thức tính diện tích tam giác.
Advertisements (Quảng cáo)

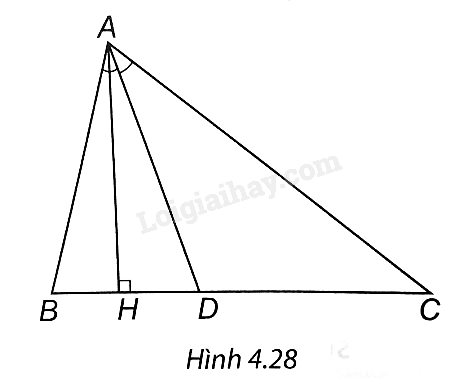
a) AD là phân giác của góc BAC, suy ra \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\) (tính chất đường phân giác của tam giác)
\(\begin{array}{l}\frac{{25 - DC}}{{DC}} = \frac{{15}}{{20}}\\\begin{array}{*{20}{l}}{20.\left( {25-DC} \right)= 15DC}\\{35.DC= 500}\end{array}\\DC = \frac{{100}}{7} \approx 14,3\,\,\left( {cm} \right).\end{array}\)
Suy ra DB = BC – DC ≈ 10,7 (cm).
b) Ta có \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{{15}}{{20}} = \frac{3}{4}.\)
∆ABD và ∆ACD có cùng đường cao AH nên tỉ số diện tích của hai tam giác bằng tỉ số độ dài của hai cạnh đáy DB và DC.
Vậy tỉ số diện tích của hai tam giác ABD và ACD là \(\frac{3}{4}.\)
