Áp dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó. Hướng dẫn giải Giải bài 5 trang 72 vở thực hành Toán 8 - Bài 15. Định lí Thalès trong tam giác . Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông,
Câu hỏi/bài tập:

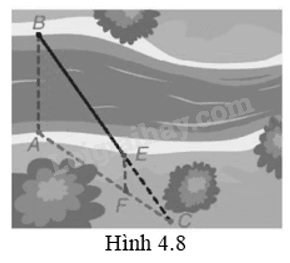
Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.8). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?
Advertisements (Quảng cáo)

Áp dụng định lý Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh cong lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Ta có AB // EF nên theo định lý Thales ta có: \(\frac{{EC}}{{EB}} = \frac{{FC}}{{AF}}\) nên \(\frac{{30}}{{EB}} = \frac{{20}}{{40}}\) suy ra EB . 20 = 40 . 30, do đó EB = 60 (m).
