Câu hỏi/bài tập:

Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.
a) Chứng minh rằng AE = DF.
b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.

Dựa vào tính chất đường trung bình của tam giác.

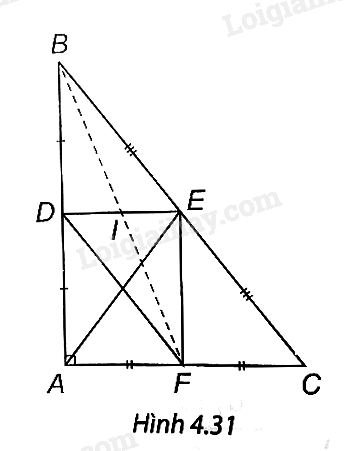
a) ∆ABC có: D là trung điểm AB, E là trung điểm BC, nên DE là đường trung bình của ∆ABC.
Advertisements (Quảng cáo)
Suy ra DE // AC và DE = \(\frac{1}{2}\)AC.
Xét tứ giác ADEF: DE // AF và DE = AF nên tứ giác ADEF là hình bình hành.
Ta lại có \(\widehat {DAF} = 90^\circ \) nên tứ giác ADEF là hình chữ nhật.
Suy ra AE = DF.
b) ∆ABC có: D là trung điểm AB, F là trung điểm AC nên DF là đường trung bình của ∆ABC.
Suy ra DF // BC và DF = \(\frac{1}{2}\)BC = BE.
Xét tứ giác BDFE: DF // BE và DF = BE nên tứ giác BDFE là hình bình hành.
Suy ra hai đường chéo DE và BF cắt nhau tại trung điểm của mỗi đường.
Ta lại có I là trung điểm của DE nên I cũng là trung điểm của BF.
Vậy B, I, F thẳng hàng.
