Bài 9 trang 106 vở thực hành Toán 8 tập 2: Cho tam giác ABC có đường cao AH. Biết AH = 12cm, CH = 9cm, BH = 16cm. Lấy M...

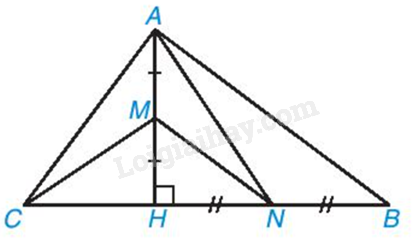
Cho tam giác ABC có đường cao AH. Biết AH = 12cm, CH = 9cm, BH = 16cm. Lấy M, N lần lượt là trung điểm của AH, BH

a) Chứng minh rằng ABC là tam giác vuông tại A

b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN

c) Tính diện tích tam giác AMN

Áp dụng định lý Pythagore, Pythagore đảo.

a) Áp dụng định lý Pythagore cho tam giác AHC vuông tại H, ta có:

AC² = AH² + CH² = 225, hay AC = 15 cm.

Áp dụng định lý Pythagore cho tam giác AHB vuông tại H, ta có:

AB² = AH² + BH² = 400, hay AB = 20 cm.

Mặt khác BC = BH + CH = 25 cm. Do đó BC² = AB² + AC². Vì vậy, theo định lý Pythagore đảo thì tam giác ABC vuông tại A.

b) Do MN // AB và AB $\bot $ AC nên MN $\bot $ AC.

$\Delta ACN$ có: AH $\bot $ CN (theo giả thiết), MN $\bot $ AC (chứng minh trên). Vậy M là trực tâm của $\Delta ACN$, do đó CM $\bot $ AN.

c) Ta có ${{S}_{AMN}}=\frac{AM.HN}{2}=\frac{AH.HB}{8}=24(c{{m}^{2}})$.