Áp dụng định lí Thalès với các cặp đường thẳng song song EF và CD, DE và BC. Giải và trình bày phương pháp giải Câu 3 trang 80 - Bài tập cuối chương IV - Vở thực hành Toán 8.
Câu hỏi/bài tập:
Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng
A. 4 cm.
B. 5 cm.
C. 6 cm.
D. 7 cm.

Áp dụng định lý Thalès với các cặp đường thẳng song song EF và CD, DE và BC.
Advertisements (Quảng cáo)

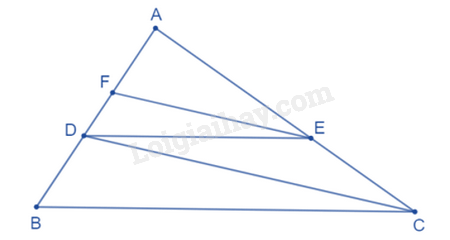
Áp dụng định lý Thalès:
• Với DE // BC (E ∈ AC) ta có: \(\frac{{A{\rm{D}}}}{{AB}} = \frac{{A{\rm{E}}}}{{AC}} = \frac{9}{{12}} = \frac{2}{3}\)
• Với EF // CD (F ∈ AB) ta có: \(\frac{{AF}}{{A{\rm{D}}}} = \frac{{A{\rm{E}}}}{{AC}} = \frac{2}{3}\)
Suy ra: \(AF = \frac{2}{3}AD = \frac{2}{3}.6 = 4(cm)\)
Vậy AF = 4 cm.
=> Chọn đáp án A.
