Câu hỏi/bài tập:

Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài với nhau tại A với \(R \ne r\). Đường nối OO’ lần lượt cắt hai đường tròn (O) và (O’) tại B và C. Đường thẳng a lần lượt tiếp xúc với hai đường tròn (O) và (O’) tại D và E. Gọi M là giao điểm của BD và CE. Chứng minh:
a) \(\widehat {DME} = 90^\circ \)
b) MA tiếp xúc với hai đường tròn (O) và (O’)
c) MD. MB = ME. MC

a) Bước 1: Chứng minh \(\widehat {BOD} = \widehat {AO’E}\).
Bước 2: Chứng minh \(\widehat B = \widehat {EAO’} = \frac{{180^\circ - \widehat {EO’A}}}{2}\).
Bước 3: Chứng minh \(\widehat C + \widehat B = 90^\circ \).
b) Bước 1: Chứng minh \(IA = ID\).
Bước 2: Chứng minh \(\Delta OAI = \Delta ODI\).
c) Chứng minh tam giác BCM đồng dạng với tam giác EDM.

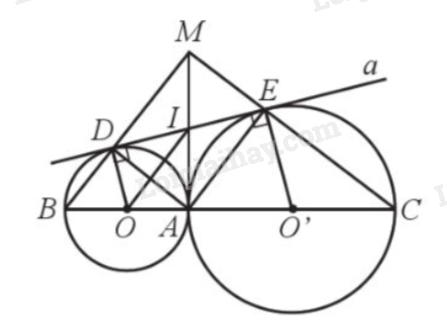
a) Ta có DE tiếp xúc với (O) và (O’) nên \(DO \bot DE,EO’ \bot DE\), do đó \(DO//EO’\),
Suy ra \(\widehat {BOD} = \widehat {AO’E}\) (2 góc so le trong). (1)
Do \(BO = DO\left( { = R} \right)\) nên tam giác BOD cân tại O, do đó \(\widehat B = \frac{{180^\circ - \widehat {BOD}}}{2}\). (2)
Do \(AO’ = EO’\left( { = r} \right)\) nên tam giác AO’E cân tại O’, do đó \(\widehat {EAO’} = \frac{{180^\circ - \widehat {EO’A}}}{2}\). (3)
Từ (1), (2), (3) suy ra \(\widehat B = \widehat {EAO’}\). (4)
Advertisements (Quảng cáo)
Xét tam giác EAC có nên tam giác EAC vuông tại E, do đó \(\widehat C + \widehat {EAO’} = 90^\circ \) (5)
Từ (4) và (5) suy ra \(\widehat C + \widehat B = 90^\circ \).
Xét tam giác MBC có \(\widehat C + \widehat B + \widehat {BMC} = 180^\circ \) hay \(90^\circ + \widehat {BMC} = 180^\circ \). Vậy \(\widehat {BMC} = 90^\circ \) hay \(\widehat {DME} = 90^\circ \).
b) Xét tam giác BDA có \(OB = OA = OD = \frac{{AB}}{2}\) nên tam giác BDA vuông tại D hay \(\widehat {BDA} = 90^\circ \), do đó \(\widehat {ADM} = 90^\circ \).
Xét tam giác AEC có \(O’E = O’A = O’C = \frac{{AC}}{2}\) nên tam giác AEC vuông tại E
hay \(\widehat {AEC} = 90^\circ \), do đó \(\widehat {AEM} = 90^\circ \).
Xét tứ giác DMEA có \(\widehat {ADM} = \widehat {DME} = \widehat {MEA} = 90^\circ \) suy ra DMEA là hình chữ nhật,
nên \(IA = ID\).
Xét 2 tam giác OAI và ODI có:
OI chung; \(OD = OA\left( { = R} \right)\); \(IA = ID\)
Suy ra \(\Delta OAI = \Delta ODI\) (c.c.c), do đó \(\widehat {OAI} = \widehat {ODI} = 90^\circ \) hay MA vuông góc với BD tại A.
Vậy MA tiếp xúc với hai đường tròn (O) và (O’).
c) Do MA tiếp xúc với hai đường tròn (O) nên MA là tiếp tuyến của (O) hay \(\widehat {BAM} = \widehat {IAD} + \widehat {DAB} = 90^\circ \).
Ta lại có: tam giác ADB cân tại D nên \(\widehat B + \widehat {DAB} = 90^\circ \), do đó \(\widehat B = \widehat {IAD}\).
Mặt khác \(\widehat {MED} = \widehat {IAD}\) (DMEA là hình chữ nhật), do đó \(\widehat {MED} = \widehat B\).
Xét 2 tam giác BCM và EDM có:
\(\widehat {MED} = \widehat B\);
\(\widehat {BMC} = 90^\circ \)
Suy ra \(\Delta BCM\backsim \Delta EDM\) (g.g), nên \(\frac{{MD}}{{EM}} = \frac{{MC}}{{MD}}\) hay \(MD.MB = ME.MC\).
