Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng. Giải chi tiết - Bài 2 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 1 - Bài 2. Tiếp tuyến của đường tròn. Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). Cho biết PB = 8, PQ = 4...

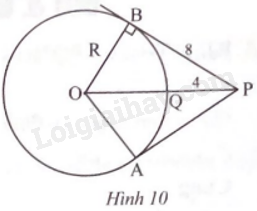
Từ điểm P ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến tiếp xúc với (O) tại A và B. Đoạn thẳng OP cắt (O) tại Q (Hình 10). Cho biết PB = 8, PQ = 4. Tính R và số đo \(\widehat {AOB}\).

Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Advertisements (Quảng cáo)

Trong \(\Delta OPB\) vuông tại B, ta có OP2 = OB2 + PB2, suy ra (R + 4)2 = R2 + 82, suy ra R = 6.
OP2 = OB2 + PB2 suy ra (R + 4)2 = R2 + 82, suy ra R = 6.
\(\sin \widehat {BOP} = \frac{{PB}}{{OP}} = \frac{8}{{6 + 4}} = \frac{4}{5}\) suy ra \(\widehat {BOP} \approx {53^o}\).
Ta lại có \(\widehat {AOB} = 2\widehat {BOP} \approx {2.53^o} = {106^o}.\)
