Dựa vào: Trên đường tròn bán kính R, độ dài l của một cung có số đo no được tính theo công thức \(l = \frac{{\pi Rn}}{{180}}\). Lời Giải - Bài 2 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1 - Bài 4. Hình quạt tròn và hình vành khuyên. Cho đường tròn (O) đường kính AB = 3 cm, (widehat {CAB}) = 30o (Hình 9). a) Tính độ dài cung BmD. b) Tính diện tích hình quạt tròn OBmD...

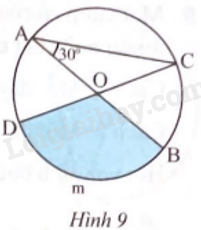
Cho đường tròn (O) đường kính AB = 3 cm, \(\widehat {CAB}\) = 30o (Hình 9).
a) Tính độ dài cung BmD.
b) Tính diện tích hình quạt tròn OBmD.

Advertisements (Quảng cáo)
Dựa vào: Trên đường tròn bán kính R, độ dài l của một cung có số đo no được tính theo công thức \(l = \frac{{\pi Rn}}{{180}}\).
Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).

a) Ta có \(\widehat {DOB} = {180^o} - 2.\widehat {CAB} = {120^o}\)
Suy ra \({{l}_{\overset\frown{BmD}}}=\frac{\pi .1,5.120}{180}=\pi \approx 3,14(cm).\)
b) \({S_{OBmD}} = \frac{{\pi {{.1,5}^2}.120}}{{180}} = \frac{3}{4}\pi \approx 2,36(c{m^2}).\)
