Dựa vào: Trên đường tròn bán kính R, độ dài l của một cung có số đo no được tính theo công thức \(l = \frac{{\pi Rn}}{{180}}\). Hướng dẫn giải - Bài 1 trang 96 sách bài tập toán 9 - Chân trời sáng tạo tập 1 - Bài 4. Hình quạt tròn và hình vành khuyên. Quan sát Hình 8 và tính a) Số đo cung AmB. b) Độ dài cung AmB. c) Diện tích hình quạt tròn OAmB. d) Diện tích hình viên phân giới hạn bởi cung AmB và dây AB...

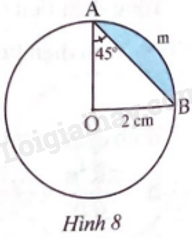
Quan sát Hình 8 và tính
a) Số đo cung AmB.
b) Độ dài cung AmB.
c) Diện tích hình quạt tròn OAmB.
d) Diện tích hình viên phân giới hạn bởi cung AmB và dây AB.

Advertisements (Quảng cáo)
Dựa vào: Trên đường tròn bán kính R, độ dài l của một cung có số đo no được tính theo công thức \(l = \frac{{\pi Rn}}{{180}}\).
Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).

a) sđ \(\overset\frown{AmB}=\widehat{AOB}={{90}^{o}}\)
b) \({{l}_{\overset\frown{AmB}}}=\frac{\pi .2.90}{180}=\pi \approx 3,14(cm)\)
c) \({S_{OAmB}} = \frac{{\pi {{.2}^2}.90}}{{360}} = \pi \approx 3,14(c{m^2})\).
d) Diện tích hình viên phân giới hạn bởi cung AmB và dây AB:
\({S_{AmB}} = {S_{OAmB}} - {S_{\Delta OAB}} = \pi - 2 \approx 1,14(c{m^2})\).
