Dựa vào: Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\). Phân tích và giải - Bài 3 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1 - Bài 4. Hình quạt tròn và hình vành khuyên. Một biểu đồ hình quạt tròn được vẽ trong đường tròn bán kính R = 15 cm (Hình 10). Tính diện tích của mỗi hình quạt tròn trong biểu đồ đó...

Một biểu đồ hình quạt tròn được vẽ trong đường tròn bán kính R = 15 cm (Hình 10). Tính diện tích của mỗi hình quạt tròn trong biểu đồ đó.
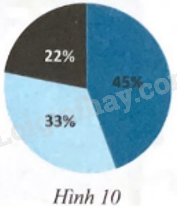

Dựa vào: Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).

Advertisements (Quảng cáo)
Diện tích hình quạt tròn ứng với số liệu 45% là:
\(45\% .\pi .{R^2} = 45\% .\pi {.15^2} = \frac{{405\pi }}{4} \approx 318,09(c{m^2})\)
Diện tích hình quạt tròn ứng với số liệu 33% là:
\(33\% .\pi .{R^2} = 33\% .\pi {.15^2} = \frac{{297\pi }}{4} \approx 233,26(c{m^2})\)
Diện tích hình quạt tròn ứng với số liệu 22% là:
\(22\% .\pi .{R^2} = 22\% .\pi {.15^2} = \frac{{99\pi }}{2} \approx 155,51(c{m^2})\).
