
a) Vẽ tam giác ABC vuông tại A, \(AB = 3cm,AC = 4cm\). Tính BC, sinB, cosB.
b) Vẽ tam giác MNP vuông tại M, \(MN = 6cm,MP = 8cm\). Hỏi hai tam giác ABC, MNP có đồng dạng không? Tính sinN, cosN.

a) - Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
- Để tính BC, ta áp dụng định lý Pythagore vào tam giác ABC vuông tại A.
b) Chứng minh hai tam giác ABC, MNP đồng dạng theo trường hợp cạnh- góc- cạnh, từ đó tính được sinN, cosN.
Advertisements (Quảng cáo)

a)
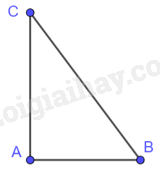
Tam giác ABC vuông tại A nên
+ \(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25\) (định lý Pythagore), suy ra \(BC = 5cm\).
+ \(\sin B = \frac{{AC}}{{CB}} = \frac{4}{5},cosB = \frac{{AB}}{{CB}} = \frac{3}{5}\).
b) Tam giác MNP và tam giác ABC có: \(\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}}\left( { = 2} \right)\) và \(\widehat A = \widehat M = {90^o}\) nên \(\Delta MNP \backsim \Delta ABC (c.g.c)\)
Do đó, \(\sin N = \sin B = \frac{4}{5};\cos N = \cos B = \frac{3}{5}\).
