Giả sử tam giác ABC cân tại A có đáy \(BC = 8cm\). Kẻ đường cao AD của tam giác cân ABC nên \(AD = 5cm\). Trả lời - Bài 4.14 trang 46 sách bài tập toán 9 - Kết nối tri thức tập 1 - Chương IV. Hệ thức lượng trong tam giác vuông. Tính tang, côtang của góc kề đáy của tam giác cân biết cạnh đáy dài 8cm, đường cao ứng với đáy dài 5cm...
Tính tang, côtang của góc kề đáy của tam giác cân biết cạnh đáy dài 8cm, đường cao ứng với đáy dài 5cm.
+ Giả sử tam giác ABC cân tại A có đáy \(BC = 8cm\). Kẻ đường cao AD của tam giác cân ABC nên \(AD = 5cm\).
+ Chứng minh AD là đường trung tuyến của tam giác ABC, từ đó tính được BD.
+ Tam giác ABD vuông tại D nên \(\tan B = \frac{{AD}}{{BD}};\cot B = \frac{{BD}}{{AD}}\).
Advertisements (Quảng cáo)
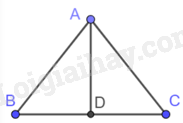
Giả sử tam giác ABC cân tại A có đáy \(BC = 8cm\). Kẻ đường cao AD của tam giác cân ABC nên \(AD = 5cm\).
Vì tam giác ABC cân tại A nên AD là đường cao đồng thời là đường trung tuyến.
Do đó, \(BD = \frac{{BC}}{2} = 4cm\).
Tam giác ABD vuông tại D nên \(\tan B = \frac{{AD}}{{BD}} = \frac{5}{4};\cot B = \frac{{BD}}{{AD}} = \frac{4}{5}\).