
Tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước (không đo trực tiếp được), biết khoảng cách từ một địa điểm C đến A và đến B là \(CA = 90m\), \(CB = 150m,\;\widehat {CAB} = {120^o}\) (làm tròn đến m) (H.4.18).
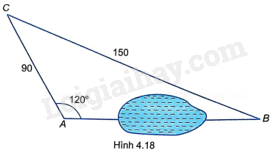

+ Kẻ đường cao CK của tam giác ABC. Chỉ ra K nằm ngoài đoạn AB.
+ Tính được \(\widehat {CAK} = {60^o}\).
+ Tam giác CAK vuông tại K nên \(AK = AC.\cos \widehat {CAK}\).
+ Áp dụng định lý Pythagore vào tam giác BKC vuông tại K để tính BK.
+ \(AB = BK - AK\).
Advertisements (Quảng cáo)

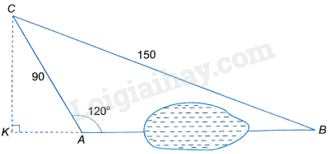
Kẻ đường cao CK của tam giác ABC.
Vì góc CAB là góc tù nên chân K của đường cao CK của tam giác ABC nằm ngoài đoạn AB.
Ta có: \(\widehat {CAK} = {180^o} - \widehat {BAC} = {180^o} - {120^o} = {60^o}\).
Tam giác CAK vuông tại K nên \(AK = AC.\cos \widehat {CAK} = 90.\cos {60^o} = 90.\frac{1}{2} = 45\left( m \right)\), \(CK = AC.\sin \widehat {CAK} = 90.\sin {60^o} = 90.\frac{{\sqrt 3 }}{2} = 45\sqrt 3 \left( m \right)\)
Tam giác BCK vuông tại K nên theo định lý Pythagore ta có:
\(B{K^2} = B{C^2} - C{K^2} = {150^2} - {\left( {45\sqrt 3 } \right)^2} = {15^2}.73\) nên \(BK = 15\sqrt {73} \left( m \right)\)
Vậy \(AB = BK - AK = 15\sqrt {73} - 45 \approx 83\left( m \right)\).
