Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh huyền gọi là côsin của \(\alpha \). Giải - Bài 4.34 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1 - Chương IV. Hệ thức lượng trong tam giác vuông. Một cầu thủ đứng cách khung thành 18m, đá quả bóng sát mặt đất, nghiêng một góc ({20^o}) so với phương vuông góc với khung thành, tới điểm M của khung thành (H. 4. 19)...
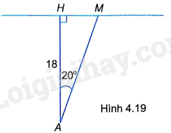
Một cầu thủ đứng cách khung thành 18m, đá quả bóng sát mặt đất, nghiêng một góc \({20^o}\) so với phương vuông góc với khung thành, tới điểm M của khung thành (H.4.19). Tính khoảng cách từ cầu thủ đến điểm M (làm tròn đến dm).
Advertisements (Quảng cáo)
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh huyền gọi là côsin của \(\alpha \)
Gọi H là hình chiếu vuông góc của cầu thủ đứng tại A lên đường thẳng chứa khung thành thì ta được tam giác AHM vuông tại H, \(AH = 18m,\widehat {HAM} = {20^o}\).
Tam giác AHM vuông tại H nên \(\cos \widehat {HAM} = \frac{{AH}}{{AM}}\) nên \(AM = \frac{{AH}}{{\cos \widehat {HAM}}} = \frac{{18}}{{\cos {{20}^o}}} \approx 19,2\left( m \right) = 192dm\).