Câu hỏi/bài tập:

Trên bờ của một cái ao cá hình tròn, người ta dựng ba cái chòi câu cá tại các điểm A, B và C. Biết rằng tam giác ABC cân tại B và có \(AB = BC = 10m,\widehat {ABC} = {120^o}\) (H.5.5).
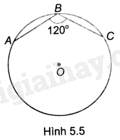
a) Tính bán kính của ao cá.
b) Tính độ dài quãng đường (men theo bờ ao) từ chòi A đến chòi B và chòi C (làm tròn kết quả đến chữ số thập phân thứ nhất).

a) + Chứng minh O thuộc đường trung trực của AC.
+ Chứng minh AC là phân giác của góc ABC, từ đo tính được góc ABO.
Advertisements (Quảng cáo)
+ Chứng minh tam giác ABO đều, suy ra \(AO = AB = 10m\).
b) Độ dài l của cung \({n^o}\) trên đường tròn (O; R) là \(l = \frac{n}{{180}}.\pi R\).

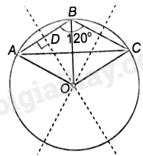
a) Gọi O là tâm của hình tròn (ao), ta có \(OA = OC\) nên O thuộc đường trung trực của AC. Mà tam giác ABC cân tại B nên đường trung trực của AC cũng là phân giác của góc ABC nên \(\widehat {ABO} = \frac{1}{2}\widehat {ABC} = {60^o}\)
Tam giác AOB có \(OA = OB,\widehat {ABO} = {60^o}\) nên tam giác AOB đều. Do đó, \(AO = AB = 10m\). Vậy bán kính của ao cá bằng 10m.
b) Độ dài quãng đường từ chòi A đến chòi B là độ dài cung nhỏ AB.
Theo phần a, ta có \(\widehat {AOB} = {60^o}\) và bán kính đường tròn là 10m nên quãng đường đó là: \(\frac{{60}}{{180}}.\pi .10 = \frac{{10\pi }}{3} \approx 10,5\left( m \right)\)
Theo phần a ta thấy hai cung AB và BC có cùng số đo bằng 60 độ nên chúng bằng nhau và độ dài của chúng cũng bằng nhau. Do đó, quãng đường từ A đến C men theo bờ bằng 2 lần độ dài cung AB. Suy ra, độ dài quãng đường A đến C men theo bờ là: \(\frac{{20\pi }}{3} \approx 20,9\left( m \right)\).
