Câu hỏi/bài tập:

Cho đường tròn (O) và điểm P.
a) Giả sử \(P \in \left( O \right)\). Vẽ đường thẳng a đi qua P và vuông góc với OP. Chứng minh rằng a là tiếp tuyến của đường tròn (O) tại P.
b) Giả sử P nằm ngoài (O). Vẽ đường tròn đường kính OP. Đường tròn vừa vẽ cắt (O) tại A và B. Chứng minh rằng PA và PB là hai tiếp tuyến của (O).

a) Vì \(P \in \left( O \right)\) và \(a \bot OP\) tại P nên a là tiếp tuyến của đường tròn (O) tại P.
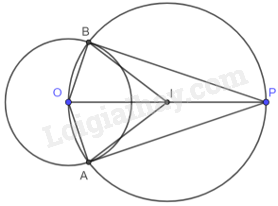
b) + Gọi I là trung điểm của OP. Suy ra, bốn điểm O, A, P, B thuộc đường tròn tâm I, đường kính OP.
+ Chứng minh tam giác OBP vuông tại B, suy ra \(OB \bot BP\) tại B, suy ra PB là tiếp tuyến của (O) tại B.
Advertisements (Quảng cáo)
+ Chứng minh tam giác OAP vuông tại A, do đó \(OA \bot AP\) tại A, suy ra PA là tiếp tuyến của (O) tại A.

a) Vì \(P \in \left( O \right)\) và \(a \bot OP\) tại P nên a là tiếp tuyến của đường tròn (O) tại P.
b) Gọi I là trung điểm của OP. Suy ra, bốn điểm O, A, P, B thuộc đường tròn tâm I, đường kính OP.
Tam giác OBP có BI là đường trung tuyến và \(BI = IP = OI = \frac{1}{2}OP\) nên tam giác OBP vuông tại B. Do đó, \(OB \bot BP\) tại B.
Vì B thuộc (O) và \(OB \bot BP\) tại B nên PB là tiếp tuyến của (O) tại B.
Tam giác OAP có AI là đường trung tuyến và \(AI = IP = OI = \frac{1}{2}OP\) nên tam giác OAP vuông tại A. Do đó, \(OA \bot AP\) tại A.
Vì A thuộc (O) và \(OA \bot AP\) tại A nên PA là tiếp tuyến của (O) tại A.
