Câu hỏi/bài tập:

Cho tam giác vuông ABC (\(\widehat A = {90^o}\)) có \(\widehat C = {30^o}\) và AB=3cm. Đường phân giác của góc B cắt AC tại D.
a) Chứng minh rằng đường tròn (D; DA) tiếp xúc với cạnh BC.
b) Tính độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn tương ứng với cung ấy.
c) Tính diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC).

a) + Qua D kẻ đường thẳng vuông góc với BC, cắt BC tại E.
+ Sử dụng tính chất tia phân giác của góc suy ra \(AD = DE\).
+ Do đó, đường tròn (D; DA) tiếp xúc với cạnh BC tại E.
b) + \(\widehat {ABC} = {90^o} - \widehat {BCA}\) nên \(\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC} = {30^o}\).
+ Tam giác ABD vuông tại A nên \(AD = AB.\tan \widehat {ABD}\).
+ \(\widehat {BDC} = {180^o} - \widehat {DBC} - \widehat {DCB}\) nên tính được số đo cung nằm trong góc BDC của đường tròn (D; DA).
+ Từ đó tính được độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn của cung nằm trong góc BDC của đường tròn (D; DA)
c) + Tam giác ABC vuông tại A nên \(AC = AB.\cot \widehat {ACB}\), từ đó tính được DC.
Diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC) là: \({S_{vk}} = \pi \left( {D{C^2} - D{A^2}} \right)\).

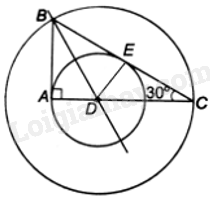
a) Qua D kẻ đường thẳng vuông góc với BC, cắt BC tại E.
Advertisements (Quảng cáo)
Vì BD là phân giác của góc ABC, AD vuông góc với AB tại A, DE vuông góc với BC tại E nên \(AD = DE\). Do đó, đường tròn (D; DA) tiếp xúc với cạnh BC tại E.
b) Tam giác ABC vuông tại A nên
\(\widehat {ABC} = {90^o} - \widehat {BCA} = {60^o}\).
Vì BA là tia phân giác của góc ABC nên
\(\widehat {ABD} = \widehat {DBC} = \frac{1}{2}\widehat {ABC} = {30^o}\).
Tam giác ABD vuông tại A nên
\(AD = AB.\tan \widehat {ABD} = 3.\tan {30^o} = \sqrt 3 \left( {cm} \right)\).
Tam giác BDC có:
\(\widehat {BDC} = {180^o} - \widehat {DBC} - \widehat {DCB} = {120^o}\).
Do đó, cung nằm trong góc BDC của đường tròn (D; DA) có số đo bằng \({120^o}\).
Độ dài cung nằm trong góc BDC của đường tròn (D; DA) là:
\(l = \frac{{120}}{{180}}.\pi .\sqrt 3 = \frac{{2\sqrt 3 \pi }}{3}\left( {cm} \right)\).
Diện tích hình quạt tròn của cung nằm trong góc BDC của đường tròn (D; DA) là:
\(S = \frac{{120}}{{360}}.\pi .{\left( {\sqrt 3 } \right)^2} = \pi \left( {c{m^2}} \right)\)
c) Tam giác ABC vuông tại A nên
\(AC = AB.\cot \widehat {ACB} = 3.\cot {30^o} = 3\sqrt 3 \left( {cm} \right)\).
Do đó, \(DC = AC - AD = 2\sqrt 3 \left( {cm} \right)\)
Diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC) là:
\({S_{vk}} = \pi \left( {D{C^2} - D{A^2}} \right) \\= \pi \left[ {{{\left( {2\sqrt 3 } \right)}^2} - {{\left( {\sqrt 3 } \right)}^2}} \right] \\= 9\pi \left( {c{m^2}} \right)\)
