Câu hỏi/bài tập:

Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm).
a) Chứng minh rằng \(PO \bot AB\).
b) Gọi C là điểm đối xứng với A qua O. Chứng minh rằng BC//PO.
c) Tính độ dài các cạnh của tam giác PAB, biết OA=3cm và OP=5cm.

a) + Chứng minh \(PA = PB\) và PO là tia phân giác của góc APB.
+ Chứng minh tam giác PAB cân tại P, suy ra PO là đường trung trực của tam giác AP nên \(PO \bot AB\).
b) + Chứng minh C thuộc (O).
+ Chứng minh tam giác ABC vuông tại B. Do đó, \(BA \bot BC\). Mà \(PO \bot AB\)(cmt) nên BC//PO.
c) + Chứng minh \(PA \bot OA\).
+ Áp dụng định lí Pythagore vào tam giác OAP vuông tại tính được PA, suy ra, \(PA = PB = 4cm\).
+ Gọi H là giao điểm của PO và AB. Theo a ta có: \(AH \bot OP\) và \(AB = 2AH\).
Advertisements (Quảng cáo)
+ \(AH.OP = OA.PA\left( { = 2{S_{\Delta AOP}}} \right)\) nên \(AH = \frac{{OA.AP}}{{OP}}\) nên tính được AB.

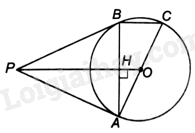
a) Vì PA và PB là hai tiếp tuyến cắt nhau tại P của (O) nên \(PA = PB\), PO là tia phân giác của góc APB.
Vì \(PA = PB\) nên tam giác PAB cân tại P. Do đó, PO là đường phân giác đồng thời là đường trung trực của tam giác ABP. Suy ra: \(PO \bot AB\).
b) Vì C là điểm đối xứng với A qua O nên \(OA = OC\). Do đó, C thuộc (O).
Vì \(OB = OC = OA = \frac{1}{2}AC\) nên tam giác BAC có trung tuyến BO có độ dài bằng nửa độ dài cạnh AC nên tam giác ABC vuông tại B. Do đó, \(BA \bot BC\). Mà \(PO \bot AB\)(cmt) nên BC//PO.
c) Vì PA tiếp xúc với (O) tại A nên \(PA \bot OA\).
Áp dụng định lí Pythagore vào tam giác OAP vuông tại A có: \(O{A^2} + A{P^2} = O{P^2}\) nên \(PA = \sqrt {O{P^2} - O{A^2}} = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right)\)
Do đó, \(PA = PB = 4cm\)
Gọi H là giao điểm của PO và AB. Theo a ta có: \(AH \bot OP\) và \(AB = 2AH\).
Ta có: \(AH.OP = OA.PA\left( { = 2{S_{\Delta AOP}}} \right)\) nên \(AH = \frac{{OA.AP}}{{OP}} = \frac{{3.4}}{5} = 2,4\left( {cm} \right)\).
Do đó, \(AB = 2AH = 2.2,4 = 4,8\left( {cm} \right)\).
