Câu hỏi/bài tập:

Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài với nhau tại A, hai điểm \(B \in \left( O \right)\) và \(C \in \left( {O’} \right)\) sao cho B và C nằm cùng phía đối với đường thẳng OO’ và OB//O’C.
a) Chứng minh góc BAC là góc vuông.
b) Cho biết \(R = 3cm\), \(R’ = 1cm\) và BC cắt OO’ tại D. Tính độ dài đoạn OD.

a) + Chứng minh tam giác AOB cân tại O nên \(\widehat {{A_1}} = \widehat {{B_1}}\).
+ Tam giác AOB có:
\(\widehat {{A_1}} + \widehat {{O_1}} + \widehat {{B_1}} = 2\widehat {{A_1}} + \widehat {{O_1}} = {180^o}\) nên \(2\widehat {{A_1}} = {180^o} - \widehat {{O_1}}\).
+ Chứng minh tam giác AO’C cân tại O’. Do đó, \(\widehat {{A_2}} = \widehat {O’CA}\).
+ Tam giác AO’C có:
\(\widehat {{A_2}} + \widehat {O{‘_1}} + \widehat {O’CA} = 2\widehat {{A_2}} + \widehat {O{‘_1}} = {180^o}\) nên \(2\widehat {{A_2}} = {180^o} - \widehat {O{‘_1}}\).
+ Do đó:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - \left( {\widehat {{O_1}} + \widehat {O{‘_1}}} \right)\) (1)
Chứng minh
\(\widehat {{O_2}} = \widehat {O{‘_1}}\), \(\widehat {{O_2}} + \widehat {{O_1}} = {180^o}\) nên \(\widehat {{O_1}} + \widehat {O{‘_1}} = {180^o}\) (2)
Từ (1) và (2) ta có:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - {180^o} = {180^o}\) nên \(\widehat {BAC} = {90^o}\).
b) + Ta có: \(OA = OB = R = 3cm,O’A = O’C = R’ = 1cm\).
+ Chứng minh \(\frac{{DO}}{{DO’}} = \frac{{OB}}{{O’C}} = \frac{3}{1}\)
+ \(DO’ = DO - OO’ = DO - \left( {OA + O’A} \right)\) \( = DO - \left( {3 + 1} \right) = DO - 4\) (4)
+ Do đó, \(\frac{{DO}}{{DO - 4}} = \frac{3}{1}\), từ đó tính được DO.
Advertisements (Quảng cáo)

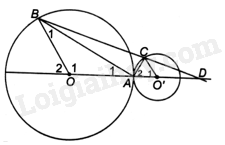
a) Vì \(OA = OB\) (bán kính của (O)) nên tam giác AOB cân tại O. Do đó, \(\widehat {{A_1}} = \widehat {{B_1}}\).
Tam giác AOB có:
\(\widehat {{A_1}} + \widehat {{O_1}} + \widehat {{B_1}} = 2\widehat {{A_1}} + \widehat {{O_1}} = {180^o}\) nên \(2\widehat {{A_1}} = {180^o} - \widehat {{O_1}}\).
Vì \(O’A = O’C\) (bán kính của (O’)) nên tam giác AO’C cân tại O’. Do đó, \(\widehat {{A_2}} = \widehat {O’CA}\).
Tam giác AO’C có:
\(\widehat {{A_2}} + \widehat {O{‘_1}} + \widehat {O’CA} = 2\widehat {{A_2}} + \widehat {O{‘_1}} = {180^o}\) nên \(2\widehat {{A_2}} = {180^o} - \widehat {O{‘_1}}\).
Do đó:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - \left( {\widehat {{O_1}} + \widehat {O{‘_1}}} \right)\) (1)
Vì OB//O’C nên \(\widehat {{O_2}} = \widehat {O{‘_1}}\) (hai góc đồng vị).
Lại có: \(\widehat {{O_2}} + \widehat {{O_1}} = {180^o}\) nên \(\widehat {{O_1}} + \widehat {O{‘_1}} = {180^o}\) (2).
Từ (1) và (2) ta có:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - {180^o} = {180^o}\) nên \(\widehat {{A_1}} + \widehat {{A_2}} = {90^o}\), suy ra \(\widehat {BAC} = {90^o}\).
b) Ta có: \(OA = OB = R = 3cm,O’A = O’C = R’ = 1cm\).
Tam giác DOB có O’C//OB nên
\(\frac{{DO}}{{DO’}} = \frac{{OB}}{{O’C}} = \frac{3}{1}\) (3)
Lại có:
\(DO’ = DO - OO’ = DO - \left( {OA + O’A} \right) \\= DO - \left( {3 + 1} \right) = DO - 4 \;(4)\)
Từ (3) và (4) ta có:
\(\frac{{DO}}{{DO - 4}} = \frac{3}{1}\), suy ra \(DO = 3\left( {DO - 4} \right)\), hay \(2DO = 12\), suy ra \(DO = 6cm\).
