Câu hỏi/bài tập:

Cho đường tròn tâm O, đường kính MN. Một đường tròn (N) cắt (O) tại A và B.
a) Chứng minh rằng MA và MB là hai tiếp tuyến của (N).
b) Đường thẳng qua N và vuông góc với NA cắt MB tại C. Chứng minh hai điểm M và N đối xứng với nhau qua OC.
c) Đường thẳng qua M và vuông góc với MA cắt NB tại D. Chứng minh ba điểm O, C và D thẳng hàng.

a) + Chứng minh \(OA = OB = OM = ON\).
+ Chứng minh tam giác MAN vuông tại A nên \(MA \bot AN\) tại A, suy ra MA là tiếp tuyến của (N).
+ Chứng minh tam giác MBN vuông tại B nên \(MB \bot BN\) tại B, suy ra MB là tiếp tuyến của (N).
b) + Chứng minh \(\widehat {{M_1}} = \widehat {{N_1}}\), \(\widehat {{M_1}} = \widehat {{M_2}}\) nên \(\widehat {{M_2}} = \widehat {{N_1}}\). Suy ra, tam giác CMN cân tại C. Do đó, CO là đường trung trực của MN. Do đó, hai điểm M và N đối xứng với nhau qua OC
c) + Vì \(MA \bot MD\) và MD//AC (cùng vuông góc với MA) nên \(\widehat {DMN} = \widehat {ANM}\)
+ Chứng minh \(\widehat {DNM} = \widehat {ANM}\) suy ra \(\widehat {DMN} = \widehat {DNM}\) nên tam giác DMN cân tại D, suy ra D nằm trên đường trung trực CO của MN. Vậy ba điểm O, C và D thẳng hàng.

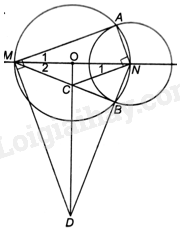
a) Vì M, A, N, B thuộc (O) nên \(OA = OB = OM = ON\).
Tam giác MAN có \(OA = OM = ON = \frac{1}{2}MN\), tức là trung tuyến OA có độ dài bằng nửa độ dài cạnh MN nên tam giác MAN vuông tại A.
Advertisements (Quảng cáo)
Do đó, \(MA \bot AN\) tại A.
Mà A thuộc (N) nên MA là tiếp tuyến của (N).
Tam giác MBN có \(OB = OM = ON = \frac{1}{2}MN\), tức là trung tuyến OB có độ dài bằng nửa độ dài cạnh MN nên tam giác MBN vuông tại B.
Do đó, \(MB \bot BN\) tại B.
Mà B thuộc (N) nên MB là tiếp tuyến của (N).
b) Vì AM//NC (cùng vuông góc với AN) nên \(\widehat {{M_1}} = \widehat {{N_1}}\).
Vì MA và MB là hai tiếp tuyến cắt nhau của (N) nên MN là phân giác của góc AMB.
Do đó, \(\widehat {{M_1}} = \widehat {{M_2}}\).
Do đó, \(\widehat {{M_2}} = \widehat {{N_1}}\).
Suy ra, tam giác CMN cân tại C.
Do đó, trung tuyến CO (vì \(OM = ON\)) đồng thời là đường trung trực của MN.
Do đó, hai điểm M và N đối xứng với nhau qua OC.
c) Vì \(MA \bot MD\) và MD//AC (cùng vuông góc với MA) nên \(\widehat {DMN} = \widehat {ANM}\).
Vì MA và MB là hai tiếp tuyến cắt nhau của (N) nên NM là phân giác của góc ANB.
Do đó, \(\widehat {DNM} = \widehat {ANM}\)
Do đó, \(\widehat {DMN} = \widehat {DNM}\) nên tam giác DMN cân tại D, suy ra D nằm trên đường trung trực CO của MN.
Vậy ba điểm O, C và D thẳng hàng.
