Câu hỏi/bài tập:

Cho tam giác cân ABC (AB=AC). Gọi (O) là đường tròn đi qua ba điểm A, B, C và E là điểm trên cung nhỏ BC sao cho $\overset\frown{BE}=\overset\frown{EC}$.
a) Chứng minh rằng ba điểm A, O, E thẳng hàng.
b) Gọi H là chân đường cao hạ từ A xuống BC. Chứng minh rằng \(AH < AB < AE\).

a) + Chứng minh \(\Delta OAB = \Delta OAC\left( {c.c.c} \right)\). Suy ra \(\widehat {AOB} = \widehat {AOC}\), suy ra $\overset\frown{AB}=\overset\frown{AC}$
+ Mà $\overset\frown{BE}=\overset\frown{EC}$. Suy ra: sđ$\overset\frown{ABE}=sđ\overset\frown{ACE}$.
+ Vì $sđ\overset\frown{ABE}+sđ\overset\frown{ACE}={{360}^{o}}$ nên sđ$\overset\frown{ABE}=sđ\overset\frown{ACE}=\frac{{{360}^{o}}}{2}={{180}^{o}}$, suy ra ba điểm A, O, E thẳng hàng.
b) + Vì EA đi qua O nên AE là đường kính của (O), AB là dây không đi qua O nên \(AB < AE\).
+ Tam giác ABH vuông tại H nên AB là cạnh huyền. Do đó, \(AH < AB\).
+ Vậy \(AH < AB < AE\).
Advertisements (Quảng cáo)

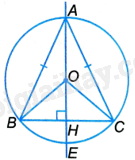
a) Tam giác OAB và tam giác OAC có: OA chung, \(AB = AC,OB = OC\) nên \(\Delta OAB = \Delta OAC\left( {c.c.c} \right)\).
Suy ra \(\widehat {AOB} = \widehat {AOC}\).
Mà AOB là góc ở tâm chắn cung nhỏ AB, AOC là góc ở tâm chắn cung nhỏ AC. Do đó, $\overset\frown{AB}=\overset\frown{AC}$
Theo giả thiết, $\overset\frown{BE}=\overset\frown{EC}$. Do đó, sđ$\overset\frown{AB}+sđ\overset\frown{BE}=sđ\overset\frown{EC}+sđ\overset\frown{AC}$
Suy ra: sđ$\overset\frown{ABE}=sđ\overset\frown{ACE}$. Mà $sđ\overset\frown{ABE}+sđ\overset\frown{ACE}={{360}^{o}}$ nên sđ$\overset\frown{ABE}=sđ\overset\frown{ACE}=\frac{{{360}^{o}}}{2}={{180}^{o}}$
Do đó, cung ABE là nửa đường tròn. Vậy ba điểm A, O, E thẳng hàng.
b) Vì EA đi qua O nên AE là đường kính của (O), AB là dây không đi qua O nên \(AB < AE\).
Tam giác ABH vuông tại H nên AB là cạnh huyền. Do đó, \(AH < AB\).
Vậy \(AH < AB < AE\).
