Câu hỏi/bài tập:

Gọi H là trung điểm của dây AB không đi qua tâm của đường tròn (O).
a) Chứng minh rằng \(OH \bot AB\).
b) Tính khoảng cách từ O đến AB, biết rằng \(AB = 8cm\) và bán kính của (O) bằng 5cm.

a) Chứng minh tam giác OAB cân tại O, suy ra OH là đường cao của tam giác ABO nên \(OH \bot AB\).
b) + Chỉ ra khoảng cách từ O đến AB là OH.
+ Áp dụng định lí Pythagore vào tam giác BOH vuông tại H tính được OH.
Advertisements (Quảng cáo)

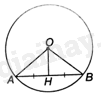
a) Tam giác ABO có: \(OA = OB\) (bán kính đường tròn (O)) nên tam giác ABO cân tại O. Do đó, OH là đường trung tuyến đồng thời là đường cao của tam giác ABO. Suy ra \(OH \bot AB\).
b) Vì \(OH \bot AB\) tại H nên khoảng cách từ O đến AB là OH.
Ta có: \(HB = \frac{{AB}}{2} = 4cm\)
Áp dụng định lí Pythagore vào tam giác BOH vuông tại H ta có: \(O{H^2} + H{B^2} = O{B^2}\)
\(OH = \sqrt {O{B^2} - H{B^2}} = \sqrt {{5^2} - {4^2}} = 3\left( {cm} \right)\)
Vậy khoảng cách từ O đến AB bằng 3cm.
