Câu hỏi/bài tập:

Một hộp đựng 6 chiếc kẹo với các nhãn hiệu A, B, C, D, E, F. Bạn Lan lấy ngẫu nhiên một chiếc kẹo cho vào cặp sách của mình. Tiếp đó bạn Hồng lấy ngẫu nhiên một chiếc kẹo từ hộp.
a) Phép thử và kết quả của phép thử là gì?
b) Mô tả không gian mẫu của phép thử. Không gian mẫu có bao nhiêu phần tử?

Sử dụng kiến thức về phép thử để tìm phép thử: Một hoặc một số hành động, thực nghiệm được tiến hành liên tiếp hay đồng thời mà kết quả của chúng không thể biết được trước khi thực hiện nhưng có thể liệt kê các kết quả có thể xảy ra, được gọi là một phép thử ngẫu nhiên, gọi tắt là phép thử.
Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Sử dụng kiến thức về không gian mẫu để tìm không gian mẫu: Tập hợp tất cả các kết quả có thể xảy ra của phép thử (gọi tắt là tập tất cả các kết quả có thể của phép thử) được gọi là không gian mẫu của phép thử.
Ta có thể tìm số phần tử của không gian mẫu bằng cách lập bảng.
Advertisements (Quảng cáo)

Phép thử là Lan lấy ngẫu nhiên một chiếc kẹo cho vào cặp sách của mình, sau đó Hồng lấy ngẫu nhiên một chiếc kẹo từ hộp.
Kết quả của phép thử là (a, b) trong đó a và b tương ứng là nhãn hiệu kẹo của chiếc kẹo mà hai bạn Lan và Hồng lấy ra trong hộp. Vì kẹo lấy ra không trả lại vào hộp nên \(a \ne b\).
Ta có bảng liệt kê các kết quả có thể xảy ra như sau:
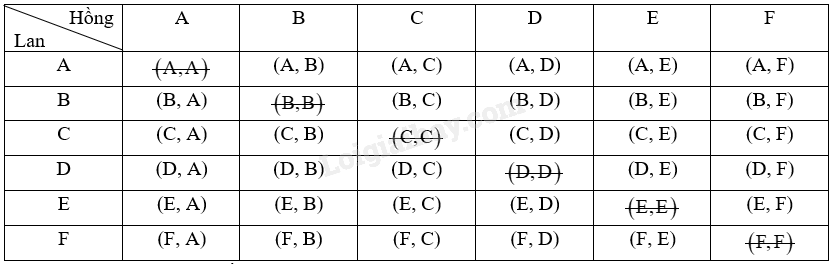
Vì \(a \ne b\) nên các cặp hai phần tử trùng nhau không được tính, tức là trong bảng ta phải xóa 6 ô: (A, A), (B, B), (C, C), (D, D), (E, E), (F, F). Do đó, không gian mẫu của phép thử là:
\(\Omega = \) {(A, B), (A, C), (A, D), (A, E), (A, F), (B, A), (B, C), (B, D), (B, E), (B, F), (C, A), (C, B), (C, D), (C, E), (C, F), (D, A), (D, B), (D, C), (D, E), (D, F), (E, A), (E, B), (E, C), (E, D), (E, F), (F, A), (F, B), (F, C), (F, D), (F, E)}.
Vậy không gian mẫu có 30 phần tử.
