Cho tam giác đều ABC cạnh bằng 3cm.. Câu 10 trang 157 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Câu 10 trang 157 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác đều ABC cạnh bằng 3cm. Bán kính của đường tròn ngoại tiếp tam giác ABC bằng:
\((A)\,2\sqrt 3 \,cm;\)
\((B)\, 2cm;\)
\((C)\,\sqrt 3 \,cm;\)
\((D)\,\sqrt 2 \,cm;\)
Hãy chọn câu trả lời đúng.
Gợi ý làm bài
Advertisements (Quảng cáo)
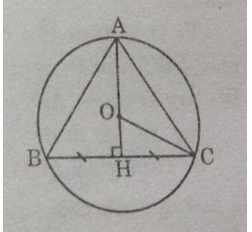
Vì O là tâm của đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ \(AH \bot BC.\), ta có: \(O \in AH\).
Trong tam giác vuông ABH, ta có:
\(AH = AB.\sin \widehat C = 3.\sin 60^\circ = {{3\sqrt 3 } \over 2}\)
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
\(OA = {2 \over 3}AH = {2 \over 3}.{{3\sqrt 3 } \over 2} = \sqrt 3 \)
Vậy chọn đáp án C.