Cho hình vuông ABCD.. Câu 11 trang 158 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Câu 11 trang 158 Sách Bài Tập (SBT) Toán 9 Tập 1.
a) Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó.
b) Tính bán kính của đường tròn đó, biết cạnh của hình vuông bằng 2dm.
Gợi ý làm bài
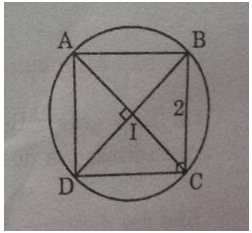
a) Gọi I là giao điểm của hai đường chéo AC và BD
Ta có:
Advertisements (Quảng cáo)
IA = IB = IC = ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} = {2^2} + {2^2} = 8\)
Suy ra: \(AC = \,2\sqrt 2 \,(cm)\)
Vậy \(R = IA = {{AC} \over 2} = {{2\sqrt 2 } \over 2} = \sqrt 2 \,(cm)\)