Tam giác ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.

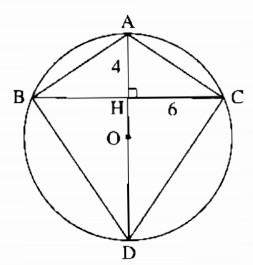
Kéo dài đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại D. Goi O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì tam giác ABC cân tại A nên AH là đường trung trực của BC. Suy ra AD là đường trung trực của BC.
Khi đó O thuộc AD hay AD là đường kính của đường tròn ngoại tiếp tam giác ABC.
Advertisements (Quảng cáo)
Tam giác ACD nội tiếp trong (O) có AD là đường kính suy ra: \(\widehat {ACD} = 90^\circ \)
Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:\(C{H^2} = HA.HD\)
Suy ra:\(HD = {{C{H^2}} \over {HA}} = {{{{\left( {{{BC} \over 2}} \right)}^2}} \over {HA}}\)
=\({{{{\left( {{{12} \over 2}} \right)}^2}} \over 4} = {{{6^2}} \over 4} = {{36} \over 4} = 9\) (cm)
Ta có: AD = AH +HD = 4 + 9 = 13 (cm)
Vậy bán kính của đường tròn (O) là: \(R = {{AD} \over 2} = {{13} \over 2} = 6,5\) (cm)
