Câu 12 trang 158 Sách Bài Tập (SBT) Toán 9 Tập 1
Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường tròn ở D.
a) Vì sao AD là đường kính của đường tròn (O)?
b) Tính số đo góc ACD.
c) Cho BC = 24cm, AC = 20cm. Tính đường cao AH và bán kính đường tròn (O).
Gợi ý làm bài
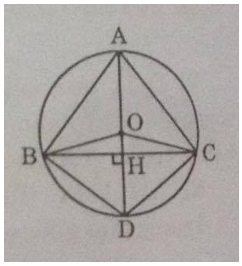
Tam giác ABC cân tại A nên AH là đường cao đồng thời cũng là đường trung trực của BC.
Vì O là tâm của đường tròn ngoại tiếp tam giác ABC nên O nằm trên đường trung trực của BC hay O thuộc AD.
Suy ra AD là đường kính của (O).
b) Tam giác ACD nội tiếp trong (O) có AD là đường kính nên suy ra \(\widehat {ACD} = 90^\circ \)
Advertisements (Quảng cáo)
c) Ta có:
\(\eqalign{
& AH \bot BC \cr
& \Rightarrow HB = HC = {{BC} \over 2} = {{24} \over 2} = 12\,(cm) \cr} \)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACH ta có:
\(A{C^2} = A{H^2} + H{C^2}\)
Suy ra:
\(\eqalign{
& A{H^2} = A{C^2} - H{C^2} \cr
& = {20^2} - {12^2} = 400 - 144 = 256 \cr} \)
\(AH = 16\,(cm)\)
Tam giác ACD vuông tại C theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(\eqalign{
& A{C^2} = AH.AD \cr
& \Rightarrow AD = {{A{C^2}} \over {AH}} = {{{{20}^2}} \over {16}} = 25\,(cm) \cr} \)
Vậy bán kính của đường tròn (O) là :
\(R = {{AD} \over 2} = {{25} \over 2} = 12,5\,(cm)\)
