Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC. Câu 9 trang 157 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Câu 9 trang 157 Sách Bài Tập (SBT) Toán 9 Tập 1
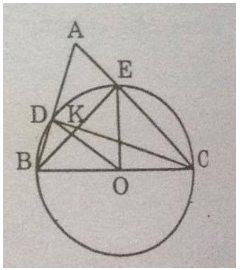
Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC, nó cắt các cạnh AB, AC theo thứ tự ở D, E.
a) Chứng minh rằng $CD \bot AB,BE \bot AC.$
b) Gọi K là giao điểm của BE và CD. Chứng minh rằng AK vuông góc với BC.
Gợi ý làm bài
Advertisements (Quảng cáo)
a) Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại D.
Suy ra: $$CD \bot AB$$
Tam giác BCE nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại E.
Suy ra: $BE \bot AC$
b) K là giao điểm của hai đường cao CD và BE nên K là trực tâm của tam giác ABC.
Suy ra: $AK \bot BC$