Cho hàm số \(y = \left( {m - 3} \right)x\).
a) Với các giá trị nào của m thì hàm số đồng biến ? Nghịch biến ?
b) Xác định giá trị của m để đồ thị hàm số đi qua điểm A(1;2).
c) Xác định giá trị của m để đồ thị hàm số đi qua điểm B(1;-2).
d) Vẽ đồ thị của hai hàm số ứng với giá trị của m tìm được ở các câu b) , c).

Điều kiện : \(m - 3 \ne 0 \Leftrightarrow m \ne 3\).
a) * Hàm số đồng biến khi hệ số \(a = m - 3 > 0 \Leftrightarrow m > 3\)
Vậy với m > 3 thì hàm số \(y = \left( {m - 3} \right)x\) đồng biến.
* Hàm số nghịch biến khi hệ số \(a = m - 3 < 0 \Leftrightarrow m < 3\)
Vậy với m < 3 thì hàm số \(y = \left( {m - 3} \right)x\) nghịch biến.
b) Đồ thị của hàm số \(y = \left( {m - 3} \right)x\) đi qua điểm A(1;2) nên tọa độ điểm A nghiệm
đúng phương trình hàm số.
Ta có: \(2 = \left( {m - 3} \right)1 \Leftrightarrow 2 = m - 3 \Leftrightarrow m = 5\)
Giá trị m = 5 thỏa mãn điều kiện bài toán .
Vậy với m = 5 thì đồ thị hàm số \(y = \left( {m - 3} \right)x\) đi qua điểm A(1;2)
Advertisements (Quảng cáo)
c) Đồ thị của hàm số \(y = \left( {m - 3} \right)x\) đi qua điểm B(1;-2) nên tọa độ điểm B nghiệm đúng phương trình hàm số.
Ta có : \(- 2 = \left( {m - 3} \right)1 \Leftrightarrow - 2 = m - 3 \Leftrightarrow m = 1\)
Giá trị m = 1 thỏa mãn điều kiện bài toán .
Vậy với m = 1 thì đồ thị hàm số \(y = \left( {m - 3} \right)x\) đi qua điểm B(1;-2).
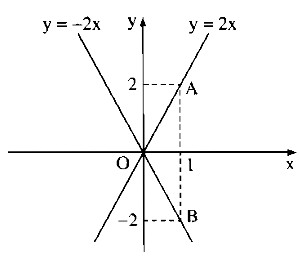
d) Khi m = 5 thì ta có hàm số: y = 2x
Khi m = 1 thì ta có hàm số: y = -2x
*Vẽ đồ thị của hàm số y = 2x
Cho x = 0 thì y = 0. Ta có: O(0;0)
Cho x = 1 thì y = 2. Ta có: A(1;2)
Đường thẳng OA là đồ thị hàm số y = 2x.
*Vẽ đồ thị của hàm số
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = -2 . Ta có : B(1;-2)
Đường thẳng OB là đồ thị của hàm số y = -2x.