Từ một hình nón, người thợ tiện có thể tiện ra một hình trụ cao nhưng “ hẹp” hoặc một hình trụ rộng nhưng “ thấp”. Trong trường hợp nào thì người thợ tiện loại bỏ ít vật liệu hơn?

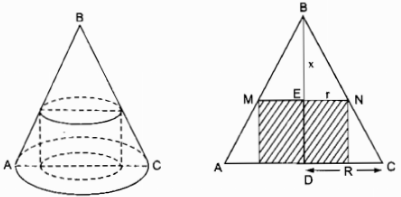
Gọi bán kính đáy hình nón là R, chiều cao hình nón là h, bán kính đáy hình trụ là r, chiều cao phần hình nón cắt đi là BE = x
\(MN//AC \Rightarrow {{ME} \over {AD}} = {{BE} \over {BD}}\) hay \({r \over R} = {x \over h} \Rightarrow r = {{Rx} \over h}\))
Thể tích hình trụ: V = πr2. h
\(V = \pi .{\left( {{{Rx} \over h}} \right)^2}.\left( {h - x} \right) = \pi .{{{R^2}{x^2}} \over {{h^2}}}(h - x)\)
Advertisements (Quảng cáo)
Phần bỏ đi của hình nón ít nhất có nghĩa là thể tích của hình trụ lớn nhất:
\(V = \pi .{{{R^2}{x^2}} \over {{h^2}}}(h - x) \Rightarrow 2V{h^2} = \pi {R^2}{x^2}(2h - 2x) \Rightarrow {{2V{h^2}} \over {\pi {R^2}}} = {x^2}(2h - 2x)\))
Vì π, R, h là các hằng số nên thể tích hình trụ lớn nhất khi và chỉ khi x2(2h – 2x) lớn nhất. Ta có: x2(2h – 2x) = x. x.(2h – 2x)
Vì x + x + (2h – 2x) = 2h là một hằng số không đổi nên tích x. x (2h – 2x) đạt giá trị lớn nhất khi và chỉ khi ba số đó bằng nhau.
\( \Rightarrow \)x = 2h -2x \(\Leftrightarrow \) 3x = 2h \(\Rightarrow \) x = \({2 \over 3}h\)
Vậy khi phần cắt bỏ ở phía trên hìnhh nón có chiều cao bằng \({2 \over 3}\) chiều cao hình nón thì phần bỏ đi là ít nhất.
