Cho hình 74, trong đó MN = PQ. Chứng minh rằng:
a) AE = AF; b) AN = AQ.

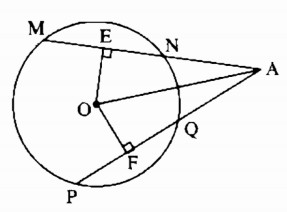
a) Nối OA
Ta có: MN = PQ (gt)
Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OAE và OAF, ta có:
\(\widehat {OEA} = \widehat {{\rm{OF}}A} = 90^\circ \)
OA chung
OE = OF ( chứng minh trên)
Advertisements (Quảng cáo)
Suy ra: ∆OAE = ∆OAF (cạnh huyền, cạnh góc vuông)
Suy ra: AE = AF
b) Ta có: OE ⊥ MN (gt)
Suy ra: \(EN = {1 \over 2}MN\) (đường kính vuông góc với dây cung) (1)
OF ⊥PQ (gt)
Suy ra: \(FQ = {1 \over 2}PQ\) (đường kính vuông góc với dây cung) (2)
Mặt khác: MN = PQ (gt) (3)
Từ (1), (2) và (3) suy ra: EN = FQ (4)
Mà AE = QF ( chứng minh trên) (5)
Từ (4) và (5) suy ra: AN + NE = AQ + QF (6)
Từ (5) và (6) suy ra: AN = AQ.
