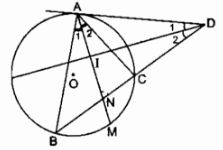
A, B, C là ba điểm thuộc đường tròn (O) sao cho tiếp tuyến tại A cắt tia BC tại D.
Tia phân giác của \(\widehat {BAC}\) cắt đường tròn ở M, tia phân giác của \(\widehat D\) cắt AM ở I. Chứng minh DI \( \bot AM\).
Giải
\(\widehat {BAM} = \widehat {MAC}\) (vì AM là tia phân giác của \(\widehat {BAC}\))
\( \Rightarrow \widehat {BM} =\) \(\overparen{CM}\) (1)
Ta có: \(\widehat {DAM} = {1 \over 2}\) sđ \(\overparen{ACM}\) (góc giữa tia tiếp tuyến và dây cung)
Advertisements (Quảng cáo)
Hay \(\widehat {DAM} = {1 \over 2}\) (sđ \(\overparen{AC}\) + sđ \(\overparen{CM}\) ) (2)
Gọi N là giao điểm của AM và BC.
Ta có: \(\widehat {ANC}\) là góc có đỉnh ở trong đường tròn (O).
\( \Rightarrow \) \(\widehat {ANC} = {1 \over 2}\) (sđ \(\overparen{AC}\) + sđ \(\overparen{BM}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {DAM} = \widehat {ANC}\) hay \(\widehat {DAN} = \widehat {AND}\)
Suy ra: ∆DAN cân tại D có DI là tia phân giác nên suy ra DI là đường cao
\( \Rightarrow \) DI ⊥ AN hay DI ⊥ AM
