Câu 5.1 trang 105 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho đường tròn tâm O bán kính R và dây AB bất kỳ. Gọi M là điểm chính giữa của cung nhỏ AB. E và F là hai điểm bất kỳ trên dây AB. Gọi C và D tương ứng là giao điểm của ME, MF của đường tròn (O). Chứng minh \(\widehat {EFD} + \widehat {ECD} = {180^0}\).
Giải
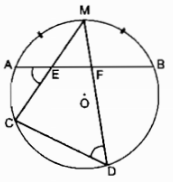
Ta có M là điểm chính giữa cung nhỏ \(\overparen{AB}\)
\( \Rightarrow \) sđ \(\overparen{MA}\) = sđ \(\overparen{MB}\) (1)
\(\widehat D = {1 \over 2}\) sđ \(\overparen{MAC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) \(\widehat D = {1 \over 2}\) (sđ \(\overparen{MA}\) + sđ \(\overparen{AC}\)) (2)
\(\widehat{AEC} = {1 \over 2}\) (sđ \(\overparen{MB}\) + sđ \(\overparen{AC}\)) (tính chất góc có đỉnh ở trong đường tròn) (3)
Từ (1), (2) và (3) suy ra: \(\widehat D = \widehat {AEC}\)
\(\widehat {AEC} + \widehat {CEF} = 180^\circ \) (kề bù)
\( \Rightarrow \)\(\widehat D + \widehat {CEF} = 180^\circ \) (4)
Trong tứ giác CEFD ta có:
\(\widehat {CEF} + \widehat D + \widehat {ECD} + \widehat {EFD} = 360^\circ \) (tổng các góc trong tứ giác) (5)
Từ (4) và (5) suy ra: \(\widehat {ECD} + \widehat {EFD} = 180^\circ \)
Câu 5.2 trang 105 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho đường tròn tâm O bán kính R. Lấy 3 điểm A, B, C trên đường tròn đó sao cho
AB = BC = CA. Gọi I là điểm bất kỳ của cung nhỏ BC (và I không trùng với B, C).
Advertisements (Quảng cáo)
Gọi M là giao điểm của CI và AB. Gọi N là giao điểm của BI và AC. Chứng minh:
a) \(\widehat {ANB} = \widehat {BCI}\)
b) \(\widehat {AMC} = \widehat {CBI}\)
Giải
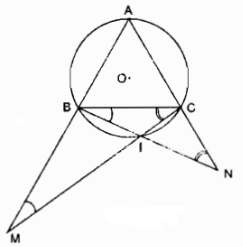
AB = AC = BC (gt)
Suy ra các cung nhỏ \(\overparen{AB}\) = \(\overparen{AC}\) = \(\overparen{BC}\) (1)
a) \(\widehat {BCI} = {1 \over 2}\) sđ \(\overparen{BI}\) (tính chất góc nội tiếp)
hay \(\widehat {BCI} = {1 \over 2}\) (sđ \(\overparen{BC}\)- sđ \(\overparen{CI}\)) (2)
Từ (1) và (2) suy ra: \(\widehat {BCI} = {1 \over 2}\) (sđ \(\overparen{AB}\)- sđ \(\overparen{CI}\) (3)
\(\widehat {ANB} = {1 \over 2}\) (sđ \(\overparen{AB}\)- sđ \(\overparen{CI}\)) (tính chất góc có ở đỉnh ở ngoài đường tròn) (4)
Từ (3) và (4) suy ra: \(\widehat {ANB} = \widehat {BCI}\)
b) \(\widehat {CBI} = {1 \over 2}\) sđ \(\overparen{CI}\)(tính chất góc nội tiếp)
Hay \(\widehat {CBI} = {1 \over 2}\) (sđ \(\overparen{BC}\)- sđ \(\overparen{BI}\)) (5)
Từ (1) và (5) suy ra: \(\widehat {CBI} = {1 \over 2}\) (sđ \(\overparen{AC}\)- sđ \(\overparen{BI}\)) (6)
\(\widehat {AMC} = {1 \over 2}\) (sđ \(\overparen{AC}\)- sđ \(\overparen{BI}\)) (tính chất góc có đỉnh ở bên ngoài đường tròn) (7)
Từ (6) và (7) suy ra: \(\widehat {AMC} = \widehat {CBI}\).
