Cho tam giác ABC vuông góc ở A. Đường tròn đường kính AB cắt BC ở D. Tiếp tuyến ở D cắt AC ở P. Chứng minh PD = PC.
Giải
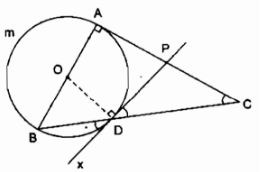
Trong đường tròn (O) ta có \(\widehat C\) là góc có đỉnh ở ngoài đường tròn.
\(\widehat C = {1 \over 2}\) (sđ \(\overparen{AmB}\) - sđ \(\overparen{AD}\)) (tính chất góc có đỉnh ở ngoài đường tròn)
Advertisements (Quảng cáo)
mà sđ \(\overparen{AmB}\) = sđ \(\overparen{ADB}\) = 1800
\(\widehat C = {1 \over 2}\) (sđ \(\overparen{ADB}\) - sđ \(\overparen{AD}\)) = \( {1 \over 2}\) (sđ \(\overparen{AD}\) + sđ \(\overparen{DB}\) - sđ \(\overparen{AD}\))= \( {1 \over 2}\) sđ \(\overparen{BD}\) (1)
\(\widehat {CDP} = \widehat {BDx}\) (đối đỉnh) (2)
\(\widehat {BDx} = {1 \over 2}\) sđ \(\overparen{BD}\) (góc giữa tia tiếp tuyến và dây cung) (3)
Từ (1), (2) và (3) suy ra: \(\widehat C = \widehat {CDP} \Rightarrow \Delta PCD\) cân tại P. Vậy PD = PC
