Chứng minh rằng dây A1A8 vuông góc với dây A3A16.. Câu 28 trang 104 Sách Bài Tập (SBT) Toán 9 Tập 2 - Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn.
Các điểm \({A_1},{A_2}...{A_{19}},{A_{20}}\) được sắp xếp theo thứ tự đó trên đường tròn (O) và chia đường tròn thành 20 cung bằng nhau. Chứng minh rằng dây \({A_1}{A_8}\) vuông góc với dây \({A_3}{A_{16}}\).
Giải
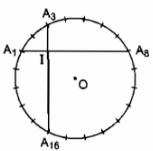
Đường tròn (O) được chia thành 20 cung bằng nhau nên số đo mỗi cung bằng
3600: 20 = 180.
Gọi giao điểm của A1A8 và A3A16 là I.
Advertisements (Quảng cáo)
Ta có: sđ \(\overparen{{A_1}{A_3}}\) \( = {2.18^0} = {36^0}\)
\(\overparen{{A_8}{A_16}}\) \( = {8.18^0} = {144^0}\)
Ta có: \(\widehat {{A_1}I{A_3}} = {1 \over 2}\) sđ \(\overparen{{A_1}{A_3}}\) + sđ \(\overparen{{A_8}{A_16}}\) (góc có đỉnh ở trong đường tròn (O))
\( \Rightarrow \) \(\widehat {{A_1}I{A_3}} = {{36^\circ + 144^\circ } \over 2} = 90^\circ \)
\( \Rightarrow \) A1A8⊥ A3A16