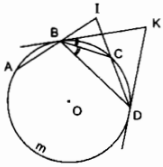
Trên đường tròn (O; R) vẽ ba dây liên tiếp bằng nhau AB, BC, CD, mỗi dây có độ dài nhỏ hơn R. Các đường thẳng AB và CD cắt nhau tại I, các tiếp tuyến của đường tròn tại B, D cắt nhau tại K.
a) Chứng minh \(\widehat {BIC} = \widehat {BKD}\)
b) Chứng minh BC là tia phân giác của \(\widehat {KBD}\).
Giải
a) \(\overparen{AB}\) = \(\overparen{BC}\) = \(\overparen{CD}\) (gt) (1)
Trong đường tròn (O) ta có \(\widehat {BKD}\) là góc có đỉnh ở ngoài đường tròn.
\( \Rightarrow \widehat {BKD} = {1 \over 2}\) (sđ \(\overparen{BAD}\) - sđ \(\overparen{BCD}\))
Advertisements (Quảng cáo)
= \({1 \over 2}\) (sđ \(\overparen{AB}\) + sđ \(\overparen{AmB}\) - sđ \(\overparen{BC}\) - sđ \(\overparen{CD}\)) (2)
Từ (1) và (2) \( \Rightarrow \widehat {BKD} = {1 \over 2}\) (sđ \(\overparen{AmB}\) - sđ \(\overparen{BC}\)) (3)
Trong đường tròn (O) ta có \(\widehat {BIC}\) là góc có đỉnh ở ngoài đường tròn.
\( \Rightarrow \widehat {BIC} = {1 \over 2}\) (sđ \(\overparen{AmB}\) - sđ \(\overparen{BC}\)) (4)
Từ (3) và (4) suy ra: \(\widehat {BIC} = \widehat {BKD}\)
b) \(\widehat {KBC} = {1 \over 2}\)sđ \(\overparen{BC}\) (tính chất giữa tia tiếp tuyến và dây cung) (5)
\(\widehat {CBD} = {1 \over 2}\) sđ \(\overparen{CD}\) (tính chất góc nội tiếp) (6)
Từ (1), (5) và (6) suy ra: \(\widehat {KBC} = \widehat {CBD}\). Vậy BC là tia phân giác của \(\widehat {KBD}\)..
