Hai dây cung AB và CD kéo dài cắt nhau tại điểm E ở ngoài đường tròn (O) (B nằm giữa A và E, C nằm giữa D và E). Cho biết \(\widehat {CDE}\) = 75 0, \(\widehat {CED} = {22^0}\), \(\widehat {AOD} = {144^0}\).
Chứng minh \(\widehat {AOB} = \widehat {BAC}\).
Giải
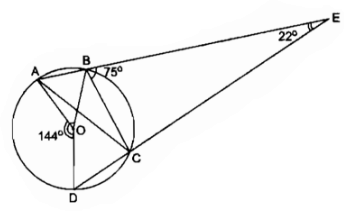
Trong đường tròn (O) ta có là góc có đỉnh ở ngoài đường tròn.
\(\widehat E = {1 \over 2}\) (sđ \(\overparen{AD}\) - sđ \(\overparen{BC}\))
sđ \(\overparen{AD}\) = \(\widehat {AOD} = 144^\circ \)
\( \Rightarrow \) 22º = \({{144^\circ - sđ \overparen{BC}} \over 2}\)
Þ sđ \(\overparen{BC}\)= 144º - 2. 22º = 100º
Advertisements (Quảng cáo)
\(\widehat {BAC} = {1 \over 2}\) sđ \(\overparen{BC}\)(tính chất nội tiếp)
\( \Rightarrow \) \(\widehat {BAC} = {1 \over 2}.100^\circ = 50^\circ \)
Trong ∆ABC ta có \(\widehat {CBE}\) là góc ngoài tại đỉnh B.
\( \Rightarrow \) \(\widehat {CBE} = \widehat {BAC} + \widehat {ACB}\) (tính chất góc ngoài của tam giác)
\( \Rightarrow \) \(\widehat {ACB} = \widehat {CBE} - \widehat {BAC} = 75^\circ - 50^\circ = 25^\circ \)
\(\widehat {ACB} = {1 \over 2}\widehat {AOB}\) (hệ quả góc nội tiếp)
\(\widehat {AOB} = 2.\widehat {ACB} = 50^\circ \)
Vậy \(\widehat {AOB} = \widehat {BAC} = 50^\circ \)
