Cho một đa giác đều n cạnh có độ dài mỗi cạnh là a. Hãy tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp đa giác đều đó.
Hướng dẫn
Tính \(\widehat {COD}\) rồi tính sin \(\widehat {COB}\) và tg \(\widehat {COB}\), từ đây tính được R và r (h.4).
Giải
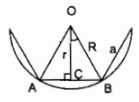
Giả sử một đa giác đều n cạnh có độ dài một cạnh là a. Gọi R là bán kính đường tròn ngoại tiếp, r bán kính đường tròn nội tiếp.
\( \Rightarrow \) OB = R; OC = r
Advertisements (Quảng cáo)
\(\widehat {AOB} = {{360^\circ } \over n} \Rightarrow \widehat {COB} = {{360^\circ } \over n}:2 = {{180^\circ } \over n}\)
Trong ∆OCB ta có: \(\widehat {OCB} = 90^\circ \)
\(\sin \widehat {COB} = {{CB} \over {OB}} = {{{a \over 2}} \over R} = {a \over {2R}} \Rightarrow 2R = {a \over {\sin {{180^\circ } \over n}}}\)
\(\Rightarrow R = {a \over {2\sin {{180^\circ } \over n}}}\)
\(\tan \widehat {COB} = {{CB} \over {OC}} = {{{a \over 2}} \over r} = {a \over {2r}} \Rightarrow 2r = {a \over {\tan {{180^\circ } \over n}}}\)
\(\Rightarrow r = {a \over {2\tan {{180^\circ } \over n}}}\)
