Tính cạnh của hình tám cạnh đều theo bán kính R của đường tròn ngoại tiếp.. Câu 49 trang 108 Sách Bài Tập (SBT) Toán 9 Tập 2 - Bài 8: Đường tròn ngoại tiếp. Đường tròn nội tiếp
Tính cạnh của hình tám cạnh đều theo bán kính R của đường tròn ngoại tiếp.
Hướng dẫn:
Cách 1: áp dụng công thức a = 2Rsin\({{180^\circ } \over n}\)
Cách 2: tính trực tiếp.
Vẽ dây AB là cạnh của một hình vuông nội tiếp đường tròn (O), gọi C là điểm chính giữa của cung nhỏ AB. Khi đó CA là cạnh của hình tám cạnh đều nội tiếp. Hãy tính CA trong tam giác vuông CAC’.
Giải
Advertisements (Quảng cáo)
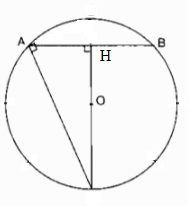
AB là cạnh của đa giác đều 8 cạnh.
Kẻ OH ⊥ AB \( \Rightarrow \) HA =HB \( = {1 \over 2}AB\)
\( \Rightarrow \widehat {HOB} = {{180^\circ } \over 8} = 22^\circ 30’\)
Trong tam giác vuông HOB ta có:
HB = OB. sin\(\widehat {HOB}\) \( \Rightarrow AB = 2.OB.\sin \widehat {HOB} = 2.R.\sin 22^\circ 30′ \approx 0,764R\)
Sacdhbaitap.com