Cho hình:
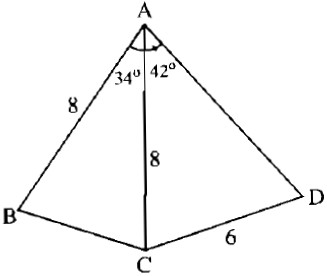
Biết:
AB = AC = 8cm, CD = 6cm, \(\widehat {BAC} = 34^\circ \) và \(\widehat {CAD} = 42^\circ .\) Tính
a) Độ dài cạnh BC;
b) \(\widehat {ADC}\);
c) Khoảng cách từ điểm B đến cạnh AD.


a) Kẻ \(AI \bot BC\)
Vì \(\Delta ABC\) cân tại A nên:
\(BI = CI = {1 \over 2}BC\)
Advertisements (Quảng cáo)
và \(\widehat {BAI} = {1 \over 2}\widehat {BAC} = {1 \over 2}.34^\circ = 17^\circ \)
Trong tam giác vuông AIB, ta có:
\(BI = AB.\sin \widehat {BAI} = 8.\sin 17^\circ \approx 2,339\left( {cm} \right)\)
\(BC = 2.BI = 2.2,339 = 4,678\left( {cm} \right)\)
b) Kẻ \(CE \bot AD\) \(\left( {E \in AD} \right)\)
Trong tam giác vuông CEA, ta có:
\(CE = AC.\sin \widehat {CAE} = 8.\sin 42^\circ \approx 5,353\left( {cm} \right)\)
Trong tam giác vuông CED, ta có:
\(\sin \widehat {ACD} = {{CE} \over {CD}} = {{5,353} \over 6} \approx 0,8922 \Rightarrow \widehat {ADC} \approx 63^\circ 9’\)
c) Kẻ \(BK \bot AD\) \(\left( {K \in AD} \right)\)
Trong tam giác vuông ABK, ta có:
\(BK = AB.\sin \widehat {BAK} = 8.\sin 75^\circ \approx 7,727\left( {cm} \right)\)
