Tìm x và y trong các hình sau:

a) Hình a
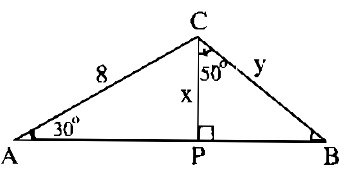
Trong tam giác vuông ACP,ta có:
\(x = CP = AC.\sin \widehat A\)
\( = 8.\sin 30^\circ = 8.{1 \over 2} = 4\)
Trong tam giác vuông BCP, ta có:
\(y = BC = {x \over {\cos \widehat {BCP}}} = {4 \over {{\rm{cos50}}^\circ }} \approx 6,223\)
b) Hình b
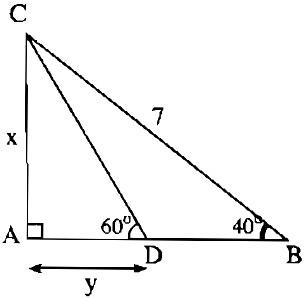
Trong tam giác vuông ABC, ta có:
\(x = AC = BC.\sin \widehat B\)
\( = 7.\sin 40^\circ \approx 4,5\)
Advertisements (Quảng cáo)
Trong tam giác vuông ACD, ta có:
\(y = AD = AC.\cot g\widehat D\)
\( \approx 4,5\cot g60^\circ = 2,598\)
c) Hình c
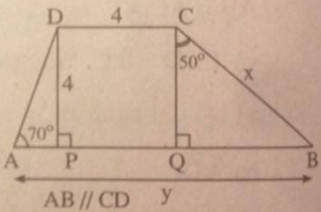
Vì tứ giác CDPQ có hai góc vuông và hai cạnh CD = DP = 4 nên nó là hình vuông. Suy ra: CD = DP = PQ = QC = 4
Trong tam giác vuông BCQ, ta có:
\(x = BC = {{CQ} \over {{\rm{cos}}\widehat {BCQ}}} = {4 \over {{\rm{cos50}}^\circ }} \approx 6,223\)
\(BQ = BC.\sin \widehat {BCQ} \approx 6,223.\sin 50^\circ = 4,767\)
Trong tam giác vuông ADP, ta có:
\(AP = DP.\cot gA = 4.\cot g70^\circ \approx 1,456\)
Ta có:
\(y = AB = AP + PQ + QB\)
\(= 1,456 + 4 + 4,767 = 10,223\).
