Cho hai đường đường tròn (O; R) và (O’;R’) cắt nhau tại A, B. Hãy so sánh R và R’ trong các trường hợp sau:
a) Số đo cung nhỏ AB của (O; R) lớn hơn số đo cung nhỏ AB của (O’; R’).
b) Số đo cung lớn AB của (O; R) nhỏ hơn số đo cung lớn AB của (O; R’).
c) Số đo hai cung nhỏ bằng nhau

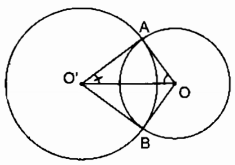
a) Trong (O; R) ta có: \(\widehat {AOB}\) = sđ cung AB (nhỏ)
Trong (O’; R) ta có: \(\widehat {AO’B}\) = sđ cung AB (nhỏ)
Vì số đo cung AB nhỏ của (O; R) lớn hơn số đo cung AB nhỏ của (O’; R’)
Suy ra: \(\widehat {AOB} > \widehat {AO’B}\) (1)
\(\Delta AOO’ = \Delta BOO’\) (cạnh – cạnh – cạnh)
\( \Rightarrow \widehat {AOO’} = \widehat {BOO’} = {1 \over 2}\widehat {AOB}\) (2)
\(\widehat {AO’O} = \widehat {BO’O} = {1 \over 2}\widehat {AO’B}\) (3)
Advertisements (Quảng cáo)
Từ (1), (2) và (3) suy ra: \(\widehat {AOO’} > \widehat {AO’O}\)
Trong \(\Delta AOO’\) ta có: \(\widehat {AOO’} > \widehat {AO’O}\)
Suy ra: O’A > OA hay R’ > R
Trường hợp hình thứ 2, ta lấy đối xứng của (O) qua trục AB ta có kết quả như hình trên.
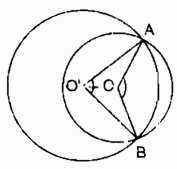
b) Trong (O; R) số đo cung lớn AB cộng với số đo cung nhỏ AB bằng 3600
Mà số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O’; R’)
Suy ra số đo cung nhỏ AB của (O; R) lớn hơn số đo cung nhỏ của (O’; R’)
Chứng minh tương tự câu a ta có: R > R’.
c) Số đo hai cung nhỏ của (O; R) và (O’; R’) bằng nhau
\( \Rightarrow \widehat {AOB} = \widehat {AO’B}\)
Suy ra: \(\widehat {AOO’} = \widehat {AO’O} \Rightarrow \Delta AOO’\) cân tại A nên OA = OA’ hay R = R’.
