Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC.
a) Tính độ dài đoạn thẳng DE.
b) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH.
c) Tính diện tích tứ giác DENM.
Gợi ý làm bài
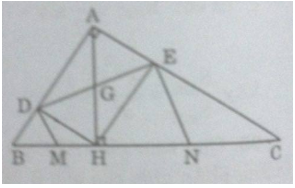
a) Ta có:
\(HD \bot AB \Rightarrow \widehat {ADH} = 90^\circ \)
\(HE \bot AC \Rightarrow \widehat {AEH} = 90^\circ \)
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật.
Suy ra: AH = DE (tính chất hình chữ nhật)
Tam giác ABC vuông tại A và có AH là đường cao.
Theo hệ thức liên hệ giữa đường cao và hình chiếu ta có:
\(\eqalign{
& A{H^2} = HB.HC = 4.9 = 36 \cr
& \Rightarrow AH = 6\,(cm) \cr} \)
Vậy DE = 6 (cm)
b) * Gọi G là giao điểm của AH và DE
Ta có: GA = GD = GH = GE (tính chất hình chữ nhật)
Suy ra tam giác GHD cân tại G
Ta có:
\(\widehat {GDH} = \widehat {GHD}\,(1)\)
\(\widehat {GDH} + \widehat {MDH} = 90^\circ \,(2)\)
\(\widehat {GHD} + \widehat {MHD} = 90^\circ \,(3)\)
Từ (1), (2) và (3) suy ra: \(\widehat {MDH} = \widehat {MHD}\,(4)\)
Suy ra tam giác MDH cân tại M \( \Rightarrow MD = MH\,(5)\)
Lại có: \(\widehat {MDH} + \widehat {MDB} = 90^\circ \,(6)\)
Advertisements (Quảng cáo)
\(\widehat {MBD} + \widehat {MHD} = 90^\circ \) (∆BDH vuong tại D) (7)
Từ (4), (6) và (7) suy ra: \(\widehat {MDB} = \widehat {MBD}\)
Suy ra tam giác MBD cân tại M \( \Rightarrow MB = MD\,(8)\)
Từ (5) và (8) suy ra: MB = MH hay M là trung điểm của BH.
*Tam giác GHE cân tại G
Ta có: \(\widehat {GHE} = \widehat {GEH}\,(9)\)
\(\widehat {GHE} + \widehat {NHE} = 90^\circ \) (10)
\(\widehat {GEH} + \widehat {NEH} = 90^\circ \) (11)
Từ (9), (10) và (11) suy ra: \(\widehat {NHE} = \widehat {NEH}\) (12)
Suy ra tam giác NEH cân tại n \( \Rightarrow NE = NH\) (13)
Lại có: \(\widehat {NEC} + \widehat {NEH} = 90^\circ \) (14)
\(\widehat {NHE} + \widehat {NCE} = 90^\circ \) (∆CEH vuông tại E) (15)
Từ (12), (14) và (15) suy ra: \(\widehat {NDC} = \widehat {NCE}\)
Suy ra tam giác NCE cân tại N \( \Rightarrow NC = NE\,(16)\)
Từ (13) và (16) suy ra: NC = NH hay N là trung điểm của CH.
c) Tam giác BDH vuông tại D có DM là đường trung tuyến nên:
\(DM = {1 \over 2}BH = {1 \over 2}.4 = 2\,(cm)\)
Tam giác CEH vuông tại E có EN là đường trung tuyến nên
\(EN = {1 \over 2}CH = {1 \over 2}.9 = 4,5\,(cm)\)
Mà \(MD \bot DE\) và \NE \bot DE\) nên MD // NE
Suy ra tứ giác DENM là hình thang
Vậy
\(\eqalign{
& {S_{DENM}} = {{DM + NE} \over 2}.DE \cr
& = {{2 + 4,5} \over 2}.6 = 19,5 \cr} \) (cm2).
